Difference between revisions of "Tours de Hanoï"
| Line 69: | Line 69: | ||
On peut fabriquer facilement un jeu de tours de Hanoï classique en mousse (papèteries spécialisées), voire en bois (avec une scie à cloche). On trouve facilement dans les magasins de jouets, des anneaux gigogne pour bébés, tout à fait adaptés à notre usage. | On peut fabriquer facilement un jeu de tours de Hanoï classique en mousse (papèteries spécialisées), voire en bois (avec une scie à cloche). On trouve facilement dans les magasins de jouets, des anneaux gigogne pour bébés, tout à fait adaptés à notre usage. | ||
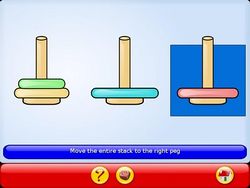
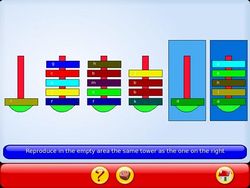
| − | Mais GCompris proposant aussi une version simplifiée en utilisant des couleurs plutôt que des tailles différentes, on peut très bien utiliser un jeu de grosses perles. Il ne faut fabriquer alors que le support des tours. On peut aussi utiliser du matériel du commerce tel que les abaques Asco | + | Mais GCompris proposant aussi une version simplifiée en utilisant des couleurs plutôt que des tailles différentes, on peut très bien utiliser un jeu de grosses perles. Il ne faut fabriquer alors que le support des tours. On peut aussi utiliser du matériel du commerce tel que les abaques Asco |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 00:50, 15 July 2007
Contents
Le problème original
Problème
Ce problème a été inventé par le mathématicien Edouard LUCAS, d’après une légende hindoue. Selon cette légende, des moines sont gardiens de trois tours. 64 disques d’or concentriques, de plus en plus petits, sont empilés dans une des tours. Les moines doivent les transférer dans une autre tour, avec une règle unique : aucun disque ne doit être posé sur un plus petit. Quand il auront terminé, ce sera la fin du monde.
Une autre légende assure que ce puzzle était utilisé dans un temple pour la discipline mentale des aspirants à l’éveil. . . C’est plutôt dans cette optique que nous l’utiliserons aussi !
Régles
- 3 poteaux ;
- un certain nombre de disques ;
- un déplacement à la fois ;
- aucun disque ne peut être posé sur un disque plus petit.
Résolution
Ce problème a toujours une solution. Il faut pour cela utiliser la troisième tour, comme lieu de stockage temporaire. Soit U le nombre de coups, n le nombre de disques, on calcule U par : U = 2n - 1.
Ce qui donne pour résultats :
| Disques | Nombre de coups |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 7 |
| 4 | 15 |
| 5 | 31 |
| ... | ... |
| 64 | 18 446 744 073 709 551 615 |
À raison d’un coup par seconde, il faudra effectivement à nos pauvres moines quelques cinq millions de millénaires pour transférer les 64 disques...
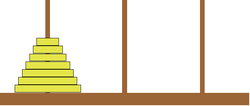
Plus rapidement, avec trois disques :
FIGURE
Proposition de démarche
Il n’est évidemment pas possible de modéliser le problème à l’école primaire et encore moins maternelle ! Néanmoins il permet d’aborder d’intéressantes notions d’algorythmique, notamment grâce à la version simplifiée de GCompris. La manipulation est une phase importante, avant d’aborder la version écran.
Matériel requis
On peut fabriquer facilement un jeu de tours de Hanoï classique en mousse (papèteries spécialisées), voire en bois (avec une scie à cloche). On trouve facilement dans les magasins de jouets, des anneaux gigogne pour bébés, tout à fait adaptés à notre usage.
Mais GCompris proposant aussi une version simplifiée en utilisant des couleurs plutôt que des tailles différentes, on peut très bien utiliser un jeu de grosses perles. Il ne faut fabriquer alors que le support des tours. On peut aussi utiliser du matériel du commerce tel que les abaques Asco