Difference between revisions of "Tours de Hanoï"
m (moved Tours de Hanoï to Tours de Hanoï) |
m |
||
| Line 1: | Line 1: | ||
[[Image:Hanoi_real.jpg|thumb|250px|Version originale]] | [[Image:Hanoi_real.jpg|thumb|250px|Version originale]] | ||
| − | [[Image:Hanoi.jpg|thumb|250px|Version | + | [[Image:Hanoi.jpg|thumb|250px|Version simplifiée.]] |
| − | = Le | + | = Le problème original = |
| − | == | + | == Problème == |
| − | [[Image:Hanoi1.png|left|thumb|250px|Tours de | + | [[Image:Hanoi1.png|left|thumb|250px|Tours de Hanoï : le problème classique]] |
| − | Ce | + | Ce problème a été inventé par le mathématicien Edouard LUCAS, d’après une légende hindoue. |
| − | Selon cette | + | Selon cette légende, des moines sont gardiens de trois tours. 64 disques d’or concentriques, de plus en plus petits, sont empilés dans une des tours. Les moines doivent les transférer dans une autre tour, avec une règle unique : aucun disque ne doit être posé sur un plus petit. Quand il auront terminé, ce sera la fin du monde. |
| − | Une autre | + | Une autre légende assure que ce puzzle était utilisé dans un temple pour la discipline mentale des aspirants à l’éveil. . . C’est plutôt dans cette optique que nous l’utiliserons aussi ! |
| − | == | + | == Régles == |
* 3 poteaux ; | * 3 poteaux ; | ||
* un certain nombre de disques ; | * un certain nombre de disques ; | ||
| − | * un | + | * un déplacement à la fois ; |
| − | * aucun disque ne peut | + | * aucun disque ne peut être posé sur un disque plus petit. |
| − | == | + | == Résolution == |
| − | Ce | + | Ce problème a toujours une solution. Il faut pour cela utiliser la troisième tour, comme lieu de |
stockage temporaire. | stockage temporaire. | ||
Soit U le nombre de coups, n le nombre de disques, on calcule U par : U = 2<sup>n</sup> - 1. | Soit U le nombre de coups, n le nombre de disques, on calcule U par : U = 2<sup>n</sup> - 1. | ||
| − | Ce qui donne pour | + | Ce qui donne pour résultats : |
{| | {| | ||
|- | |- | ||
| Line 52: | Line 52: | ||
|} | |} | ||
| − | + | À raison d’un coup par seconde, il faudra effectivement à nos pauvres moines quelques cinq millions de millénaires pour transférer les 64 disques... | |
Plus rapidement, avec trois disques : | Plus rapidement, avec trois disques : | ||
| Line 58: | Line 58: | ||
FIGURE | FIGURE | ||
| − | = Proposition de | + | = Proposition de démarche = |
| − | Il | + | Il n’est évidemment pas possible de modéliser le problème à l’école primaire et encore moins |
| − | maternelle ! | + | maternelle ! Néanmoins il permet d’aborder d’intéressantes notions d’algorythmique, notamment |
| − | + | grâce à la version simplifiée de GCompris. La manipulation est une phase importante, avant d’aborder | |
| − | la version | + | la version écran. |
| − | == | + | == Matériel requis == |
| − | On peut fabriquer facilement un jeu de tours de | + | On peut fabriquer facilement un jeu de tours de Hanoï classique en mousse (papèteries spécialisées), voire en bois (avec une scie à cloche). On trouve facilement dans les magasins de jouets, des anneaux gigogne pour bébés, tout à fait adaptés à notre usage. |
| − | Mais GCompris proposant aussi une version | + | Mais GCompris proposant aussi une version simplifiée en utilisant des couleurs plutôt que des tailles différentes, on peut très bien utiliser un jeu de grosses perles. Il ne faut fabriquer alors que le support des tours. On peut aussi utiliser du matériel du commerce tel que les abaques Asco™. Une autre possibilité sympathique est d’utiliser des épingles à linge de couleur, à condition de veiller àa ce que l’enfant ne décroche que les pinces normalement accessibles. |
| − | == | + | == Activités == |
{| | {| | ||
|- | |- | ||
| − | ! | + | !Activité |
!Objectifs | !Objectifs | ||
| − | ! | + | !Déroulement |
| − | ! | + | !Évaluation |
|- | |- | ||
|En rang ! (2) | |En rang ! (2) | ||
|Comparer, classer et ranger des objets selon leur taille, leur masse ou leur contenance. | |Comparer, classer et ranger des objets selon leur taille, leur masse ou leur contenance. | ||
| − | |On dispose de trois bancs perpendiculaires au mur, dont | + | |On dispose de trois bancs perpendiculaires au mur, dont l’extrémité touche mur. Les enfant se rangent du plus petit au plus grand, le plus grand contre le mur. Ils doivent reconsituer la même disposition sur |
| − | le | + | le deuxième banc, avec les règles suivantes : |
* on ne double pas ; | * on ne double pas ; | ||
| − | * on sort par | + | * on sort par l’extrémité libre du banc ; |
* aucun enfant ne peut se placer devant un plus petit que lui. | * aucun enfant ne peut se placer devant un plus petit que lui. | ||
Commencer par deux, puis trois enfants. | Commencer par deux, puis trois enfants. | ||
| − | Ne pas | + | Ne pas dépasser 4. |
|Par le groupe | |Par le groupe | ||
|- | |- | ||
|Perles | |Perles | ||
| − | |Savoir reproduire | + | |Savoir reproduire l’organisation dans l’espace d’un ensemble limité d’objets (en les manipulant, en les représentant). |
| − | |Reproduire une | + | |Reproduire une séquence de perles donnée à partir des perles disposées sur trois tiges : |
| − | * on | + | * on déplace une perle à la fois ; |
* on ne garde pas de perle dans la main, ni sur la table. | * on ne garde pas de perle dans la main, ni sur la table. | ||
| − | Attention | + | Attention à ce que la manipulation soit effectivement possible : veiller à ce que les perles du modèle |
soient effectivement dans le jeu. | soient effectivement dans le jeu. | ||
| − | | | + | |Séquence identique à l’original. |
|- | |- | ||
| − | |GCompris - Tours de | + | |GCompris - Tours de Hanoï simplifiées |
|Id. | |Id. | ||
| − | |Utilisation de GCompris par groupe de deux | + | |Utilisation de GCompris par groupe de deux élèves, puis individuellement. |
| − | |Fiche de suivi ou | + | |Fiche de suivi ou évaluation intégrée au logiciel (V 7.0) |
|- | |- | ||
| − | |Tours de | + | |Tours de Hanoï classiques |
|Id. | |Id. | ||
| − | | | + | |Résoudre le problème classique avec trois, voire quatre anneaux. |
| − | | | + | |Réussite du problème. Il est intéressant de savoir si le résultat est |
| − | obtenu | + | obtenu après tâtonnements ou bien directement par une démarche algorythmique |
| − | + | maîtrisée (au bout de quelques essais). | |
|- | |- | ||
| − | |Tours de | + | |Tours de Hanoï virtuelles avec GCompris |
|Id. | |Id. | ||
| − | |Utilisation de GCompris par groupe de deux | + | |Utilisation de GCompris par groupe de deux élèves, puis individuellement. |
| − | |Fiche de suivi ou | + | |Fiche de suivi ou évaluation intégrée au logiciel (V 7.0) |
|- | |- | ||
| − | |Tours de | + | |Tours de Hanoï - Papier découpé |
|Id. | |Id. | ||
|Une fois le principe du jeu acquis, il est possible de demander aux | |Une fois le principe du jeu acquis, il est possible de demander aux | ||
| − | enfants de reconstituer les | + | enfants de reconstituer les étapes de la résolution du problème avec trois disques, à |
| − | + | l’aide de bandes de papier ou en coloriant les disques vides (cf. fiche d’activité | |
suivante). | suivante). | ||
| − | | | + | |Réussite de la fiche d’activité. |
|} | |} | ||
Revision as of 00:31, 10 March 2012
Contents
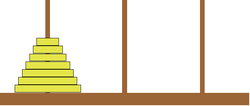
Le problème original
Problème
Ce problème a été inventé par le mathématicien Edouard LUCAS, d’après une légende hindoue. Selon cette légende, des moines sont gardiens de trois tours. 64 disques d’or concentriques, de plus en plus petits, sont empilés dans une des tours. Les moines doivent les transférer dans une autre tour, avec une règle unique : aucun disque ne doit être posé sur un plus petit. Quand il auront terminé, ce sera la fin du monde.
Une autre légende assure que ce puzzle était utilisé dans un temple pour la discipline mentale des aspirants à l’éveil. . . C’est plutôt dans cette optique que nous l’utiliserons aussi !
Régles
- 3 poteaux ;
- un certain nombre de disques ;
- un déplacement à la fois ;
- aucun disque ne peut être posé sur un disque plus petit.
Résolution
Ce problème a toujours une solution. Il faut pour cela utiliser la troisième tour, comme lieu de stockage temporaire. Soit U le nombre de coups, n le nombre de disques, on calcule U par : U = 2n - 1.
Ce qui donne pour résultats :
| Disques | Nombre de coups |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 7 |
| 4 | 15 |
| 5 | 31 |
| ... | ... |
| 64 | 18 446 744 073 709 551 615 |
À raison d’un coup par seconde, il faudra effectivement à nos pauvres moines quelques cinq millions de millénaires pour transférer les 64 disques...
Plus rapidement, avec trois disques :
FIGURE
Proposition de démarche
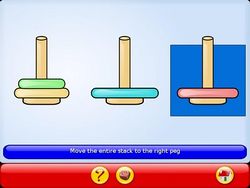
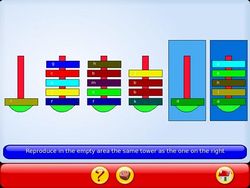
Il n’est évidemment pas possible de modéliser le problème à l’école primaire et encore moins maternelle ! Néanmoins il permet d’aborder d’intéressantes notions d’algorythmique, notamment grâce à la version simplifiée de GCompris. La manipulation est une phase importante, avant d’aborder la version écran.
Matériel requis
On peut fabriquer facilement un jeu de tours de Hanoï classique en mousse (papèteries spécialisées), voire en bois (avec une scie à cloche). On trouve facilement dans les magasins de jouets, des anneaux gigogne pour bébés, tout à fait adaptés à notre usage.
Mais GCompris proposant aussi une version simplifiée en utilisant des couleurs plutôt que des tailles différentes, on peut très bien utiliser un jeu de grosses perles. Il ne faut fabriquer alors que le support des tours. On peut aussi utiliser du matériel du commerce tel que les abaques Asco™. Une autre possibilité sympathique est d’utiliser des épingles à linge de couleur, à condition de veiller àa ce que l’enfant ne décroche que les pinces normalement accessibles.
Activités
| Activité | Objectifs | Déroulement | Évaluation |
|---|---|---|---|
| En rang ! (2) | Comparer, classer et ranger des objets selon leur taille, leur masse ou leur contenance. | On dispose de trois bancs perpendiculaires au mur, dont l’extrémité touche mur. Les enfant se rangent du plus petit au plus grand, le plus grand contre le mur. Ils doivent reconsituer la même disposition sur
le deuxième banc, avec les règles suivantes :
Commencer par deux, puis trois enfants. Ne pas dépasser 4. |
Par le groupe |
| Perles | Savoir reproduire l’organisation dans l’espace d’un ensemble limité d’objets (en les manipulant, en les représentant). | Reproduire une séquence de perles donnée à partir des perles disposées sur trois tiges :
Attention à ce que la manipulation soit effectivement possible : veiller à ce que les perles du modèle soient effectivement dans le jeu. |
Séquence identique à l’original. |
| GCompris - Tours de Hanoï simplifiées | Id. | Utilisation de GCompris par groupe de deux élèves, puis individuellement. | Fiche de suivi ou évaluation intégrée au logiciel (V 7.0) |
| Tours de Hanoï classiques | Id. | Résoudre le problème classique avec trois, voire quatre anneaux. | Réussite du problème. Il est intéressant de savoir si le résultat est
obtenu après tâtonnements ou bien directement par une démarche algorythmique maîtrisée (au bout de quelques essais). |
| Tours de Hanoï virtuelles avec GCompris | Id. | Utilisation de GCompris par groupe de deux élèves, puis individuellement. | Fiche de suivi ou évaluation intégrée au logiciel (V 7.0) |
| Tours de Hanoï - Papier découpé | Id. | Une fois le principe du jeu acquis, il est possible de demander aux
enfants de reconstituer les étapes de la résolution du problème avec trois disques, à l’aide de bandes de papier ou en coloriant les disques vides (cf. fiche d’activité suivante). |
Réussite de la fiche d’activité. |